Options Risk and Hedging

What is Tail Risk

In financial statistics, asset return distributions often deviate from a perfect normal distribution. Instead, they exhibit “fat-tailed distributions,” where extreme events are statistically unlikely but can have enormous impact and destructive power when they occur.

For options traders:

• Seller strategies (such as naked short Puts, Iron Condors, Strangles) have high win rates but may suffer catastrophic losses during tail events
• Buyer strategies (such as Long Puts, Straddles) can hedge against or profit from tail risk

Example:

Assume you sold a BTC $80,000 Put (receiving $1,000 premium) when current price is $100,000. You believe BTC won’t crash that quickly.

But if the market crashes:

• BTC drops to $60,000 within days
• You must buy one BTC at $80,000 when market price is only $60,000
• Loss = $20,000 - $1,000 = $19,000

Your expected small premium ($1,000) turns into a massive loss, nearly 20 times larger → a typical “tail risk” explosion.

Forms of Tail Risk:

How to Address and Manage Tail Risk:

Conclusion:

Tail risk is an extremely destructive hidden bomb in options strategies, especially fatal for seller strategies. You cannot ignore risk exposure just because of “high win rates.” Truly stable options trading must be a strategy system that can survive even in extreme market conditions.

What is Whalley-Wilmott Asymptotic Optimal Hedging Model?

The Whalley-Wilmott model, developed by Paul Wilmott and Anne Whalley, is a dynamic hedging method primarily designed to minimize hedging cost risk, especially when transaction costs exist. This model is classified as an asymptotically optimal hedging strategy, suitable for portfolios that require high-frequency hedge adjustments.

Core Concept

Ideally, under the Black-Scholes model, option sellers can completely hedge risk through continuous adjustment (Continuous Delta Hedging). However, in reality:

• Transaction costs (fees, bid-ask spreads) make frequent rebalancing expensive
• Discrete hedging cannot completely eliminate risk

Goal of the Whalley-Wilmott Model:

Find optimal balance between transaction costs and risk - hedging frequency shouldn’t be too high (avoid excessive costs) or too low (avoid excessive risk exposure).

Key Formula

Whalley-Wilmott provides an optimal hedging interval (No-Trade Region) - adjustments are made only when underlying asset price moves outside this interval:

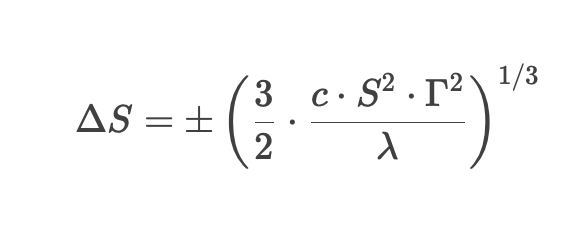
In this formula:

• Δ S = price change threshold that triggers hedging
• c = transaction cost (as a proportion)
• S = underlying asset price
• Γ = Gamma of the option (second-order sensitivity)
• λ = Risk Aversion coefficient

Strategy Rules:

1.Calculate current option’s Delta (hedge ratio)
2.Set a tolerance interval (No-Trade Region) - no hedging as long as asset price stays within interval
3.When price moves outside interval, adjust position to return Delta to target value
4.Features

5.Comparison with Other Hedging Methods:

6.Summary

• The Whalley-Wilmott model is a dynamic hedging optimization method with awareness towards transaction costs
• Reduces unnecessary rebalancing while controlling risk by setting “no-trade regions”
• Suitable for high Gamma options or high transaction cost environments, a realistic improvement on the Black-Scholes model

This model has important applications in quantitative options trading and risk management, especially suitable for institutional investors needing to balance transaction costs and risk exposure.