Riesgo y cobertura en opciones

¿Qué es el riesgo de cola?

En estadística financiera, las distribuciones de los rendimientos de activos rara vez se ajustan a una normalidad perfecta. En su lugar, presentan colas gruesas, donde los eventos extremos, si bien poco frecuentes, pueden tener un impacto devastador y consecuencias muy graves cuando suceden.

Para quienes operan con opciones:

• Las estrategias vendedoras (como venta de puts desnudos, iron condors o strangles) suelen tener una alta tasa de aciertos, pero pueden acarrear pérdidas catastróficas ante un evento de cola
• Las estrategias compradoras (como comprar puts o straddles) permiten cubrirse frente al riesgo de cola o incluso obtener beneficios de él

Ejemplo:

Supongamos que vende una put de BTC a 80.000 $ (cobrando una prima de 1.000 $) cuando el precio está en 100.000 $. Considera improbable que BTC sufra una caída tan brusca.

Pero si el mercado se hunde:

• BTC cae a 60.000 $ en cuestión de días
• Está obligado a adquirir un BTC a 80.000 $ aunque el precio de mercado sea 60.000 $
• Pérdida = 20.000 $ - 1.000 $ = 19.000 $

Esa prima modesta esperada (1.000 $) se transforma en una pérdida enorme, casi 20 veces mayor: una explosión clásica de “riesgo de cola”.

Tipos de riesgo de cola:

Cómo abordar y gestionar el riesgo de cola:

Conclusión:

El riesgo de cola es una amenaza latente de alto poder destructivo en las estrategias con opciones y resulta especialmente crítico para quienes emplean estrategias vendedoras. No se puede ignorar la exposición al riesgo solo por lograr tasas de éxito elevadas. La verdadera gestión estable de opciones requiere un sistema de estrategias capaz de resistir incluso las condiciones de mercado más extremas.

¿Qué es el modelo de cobertura óptima asintótica de Whalley-Wilmott?

El modelo Whalley-Wilmott, desarrollado por Paul Wilmott y Anne Whalley, propone una cobertura dinámica diseñada para minimizar el riesgo de coste en la cobertura, especialmente en presencia de costes de transacción. Este modelo se clasifica como una estrategia de cobertura óptima asintótica, indicada para carteras que requieren ajustes de cobertura muy frecuentes.

Concepto clave

En principio, según el modelo Black-Scholes, quien vende opciones podría cubrir el riesgo de manera completa mediante ajustes continuos (cobertura delta continua). Sin embargo, en la práctica:

• Los costes de transacción (comisiones y horquillas) hacen que el rebalanceo frecuente resulte muy costoso
• La cobertura discreta nunca elimina el riesgo por completo

El objetivo del modelo Whalley-Wilmott:

Encontrar un equilibrio óptimo entre los costes de transacción y la exposición al riesgo: la frecuencia de cobertura no debe ser ni demasiado alta (para evitar costes exagerados) ni demasiado baja (para no quedar excesivamente expuesto al riesgo).

Fórmula clave

Whalley-Wilmott define un intervalo óptimo de cobertura (“región de no negociación”): solo se ajusta la cobertura cuando el precio del activo subyacente sale de dicho intervalo:

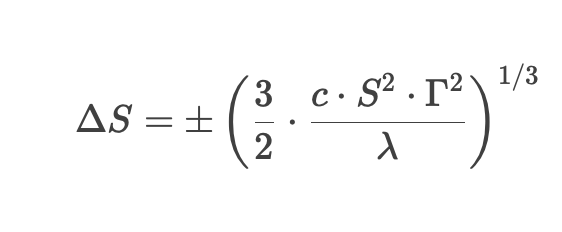
La fórmula contiene:

• Δ S = umbral de variación de precio que activa la cobertura
• c = coste de transacción (en proporción)
• S = precio del activo subyacente
• Γ = Gamma de la opción (sensibilidad de segundo orden)
• λ = coeficiente de aversión al riesgo

Principios de la estrategia:

1. Calcular el delta (ratio de cobertura) de la opción
2. Definir un intervalo de tolerancia (región de no negociación): mientras el precio del activo permanezca dentro, no se cubre
3. Si el precio rebasa ese margen, ajustar la posición para devolver el delta al objetivo
4. Características

5. Comparativa con otros métodos de cobertura:

6. Resumen

• El modelo Whalley-Wilmott es una metodología de optimización dinámica de coberturas que integra el coste de transacción
• Permite reducir rebalanceos innecesarios y controlar la exposición estableciendo “regiones de no negociación”
• Especialmente relevante en opciones con gamma alta o en mercados con costes de transacción elevados; constituye una mejora realista respecto al modelo de Black-Scholes

Este modelo resulta muy valioso en trading cuantitativo de opciones y gestión del riesgo, siendo especialmente adecuado para inversores institucionales que deben equilibrar costes operativos y exposición al riesgo.