Risque lié aux options et stratégies de couverture

Qu’est-ce que le risque de queue ?

En finance quantitative, la distribution des rendements d’actifs s’écarte souvent du modèle de distribution normale. On observe à la place des « distributions à queue épaisse », où les événements extrêmes restent rares d’un point de vue statistique, mais lorsqu’ils se produisent, leur impact et leur pouvoir destructeur peuvent être majeurs.

Pour les opérateurs d’options :

• Les stratégies vendeuses (vente à découvert de put, Iron Condor, Strangle, etc.) présentent généralement un taux de succès élevé, mais sont exposées à des pertes catastrophiques en cas d’événement de queue
• Les stratégies acheteuses (Long Put, Straddle, etc.) permettent de se couvrir contre le risque de queue ou d’en tirer profit

Exemple :

Supposons que vous ayez vendu une option Put BTC 80 000 $ (prime reçue : 1 000 $), alors que le cours actuel est de 100 000 $. Vous êtes convaincu que le BTC ne chutera pas aussi brutalement.

Mais en cas de krach :

• Le BTC chute à 60 000 $ en seulement quelques jours
• Vous êtes obligé d’acheter un BTC à 80 000 $ alors que sa valeur de marché n’est plus que de 60 000 $
• Perte = 20 000 $ - 1 000 $ = 19 000 $

La modeste prime attendue (1 000 $) se transforme en une perte massive, près de 20 fois supérieure : un exemple classique d’explosion du « risque de queue ».

Formes du risque de queue :

Comment anticiper et gérer le risque de queue :

Conclusion :

Le risque de queue est un danger caché majeur dans toute stratégie sur options, et s’avère particulièrement fatal pour les vendeurs. Ne vous laissez pas tromper par « des taux de réussite élevés » au point d’ignorer votre exposition au risque. Pour que le trading d’options soit réellement robuste, il faut une stratégie capable de survivre même dans des conditions extrêmes de marché.

Qu’est-ce que le modèle optimal asymptotique de couverture de Whalley-Wilmott ?

Le modèle Whalley-Wilmott, conçu par Paul Wilmott et Anne Whalley, constitue une méthode de couverture dynamique visant principalement à réduire le risque de coût de couverture, notamment lorsque des frais de transaction existent. Ce modèle, reconnu comme une stratégie de couverture optimale asymptotique, s’adresse aux portefeuilles nécessitant des ajustements de couverture fréquents.

Concept clé

Dans le cadre théorique du modèle Black-Scholes, un vendeur d’options peut totalement se couvrir via des ajustements continus (couverture delta permanente). Cependant, en pratique :

• Les frais de transaction (commissions, fourchettes de prix) rendent les ajustements fréquents coûteux
• La couverture par paliers n’élimine pas complètement le risque

L’objectif du modèle Whalley-Wilmott :

Atteindre un équilibre optimal entre coût de transaction et risque : la fréquence de couverture ne doit être ni trop élevée (pour limiter les frais), ni trop faible (pour ne pas accroître le risque).

Formule essentielle

Whalley-Wilmott définit un intervalle optimal d’ajustement (zone de non-intervention) : on ne procède à l’ajustement que lorsque le prix de l’actif sous-jacent sort de cette zone.

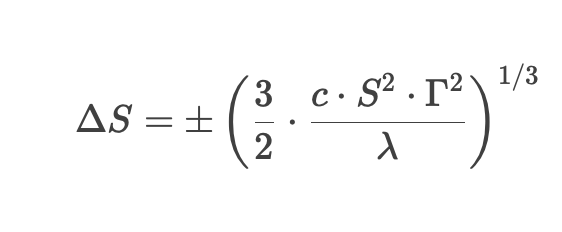
Dans cette formule :

• Δ S = seuil de variation du prix qui déclenche l’ajustement
• c = coût de transaction (en proportion)
• S = prix de l’actif sous-jacent
• Γ = Gamma de l’option
• λ = paramètre d’aversion au risque

Principes de la stratégie :

1. Calculer le delta de l’option
2. Définir une zone de tolérance (zone de non-intervention) : tant que le prix de l’actif reste dans cette zone, il n’y a pas de couverture
3. Dès que le prix franchit la limite, ajuster la position pour ramener le delta à la cible
4. Caractéristiques

5. Comparatif avec d’autres méthodes de couverture :

6. Résumé

• Le modèle Whalley-Wilmott est une méthode dynamique d’optimisation de la couverture tenant compte explicitement des coûts de transaction
• En définissant des « zones de non-intervention », il limite les réajustements inutiles tout en contrôlant le niveau de risque
• Ce modèle s’avère particulièrement efficace pour les options à gamma élevé ou dans les environnements où les coûts de transaction sont importants, offrant une amélioration pragmatique du modèle Black-Scholes

Son application est essentielle dans le trading quantitatif d’options et la gestion des risques. Il répond parfaitement aux besoins des investisseurs institutionnels souhaitant optimiser la balance entre frais de transaction et exposition au risque.